CPP Matrix Addition using Dev-C++

Source Code:

#include <iostream>

using namespace std;

/*
For Matrix addition it is necessary that
No of Rows and Columns in first Matrix
= No of Rows and Columns in second Matrix
For example:
Matrix A = 3 x 3
Matrix B = 3 x 3
Then addition is possible
*/
int main(int argc, char** argv) {
     
     // initialization of matrices
     int matA[3][3] = {{5,7,2}  // matrix of order 3 x 3
                       ,{6,1,9}
                       ,{5,2,8}};
    int matB[3][3] = {{1,5,2}   // matrix of order 3 x 3
                      ,{8,7,6}
                      ,{4,3,2}};

    cout<<"Matrix A:"<<endl;  // First matrix printing           
    for( int i = 0 ; i< 3; i++) {
        for (int j = 0;  j<3; j++) {
            cout<<matA[i][j]<<"\t";  // \t (tab) used for space
        }
        cout<<endl;  // This will print next row in new line 
    }

   cout<<"Matrix B:"<<endl;  // Second matrix printing           
    for( int i = 0 ; i< 3; i++) {
        for (int j = 0;  j<3; j++) {
            cout<<matA[i][j]<<"\t";  // \t (tab) used for space
        }
        cout<<endl;  // This will print next row in new line 
    }

    int sum;
    cout<<"Matrix Addition:"<<endl; 

    for( int i = 0 ; i< 3; i++) {  // loop upto no of rows
        for (int j = 0;  j<3; j++) {  // loop upto no of columns
            sum = 0; // To save new result assigning 0
            sum = matA[i][j] + matB[i][j];
            cout<<sum<<"\t";  // \t (tab) used for space
        }
        cout<<endl; // This will print next row in new line 
    }

return 0;
}

Output:

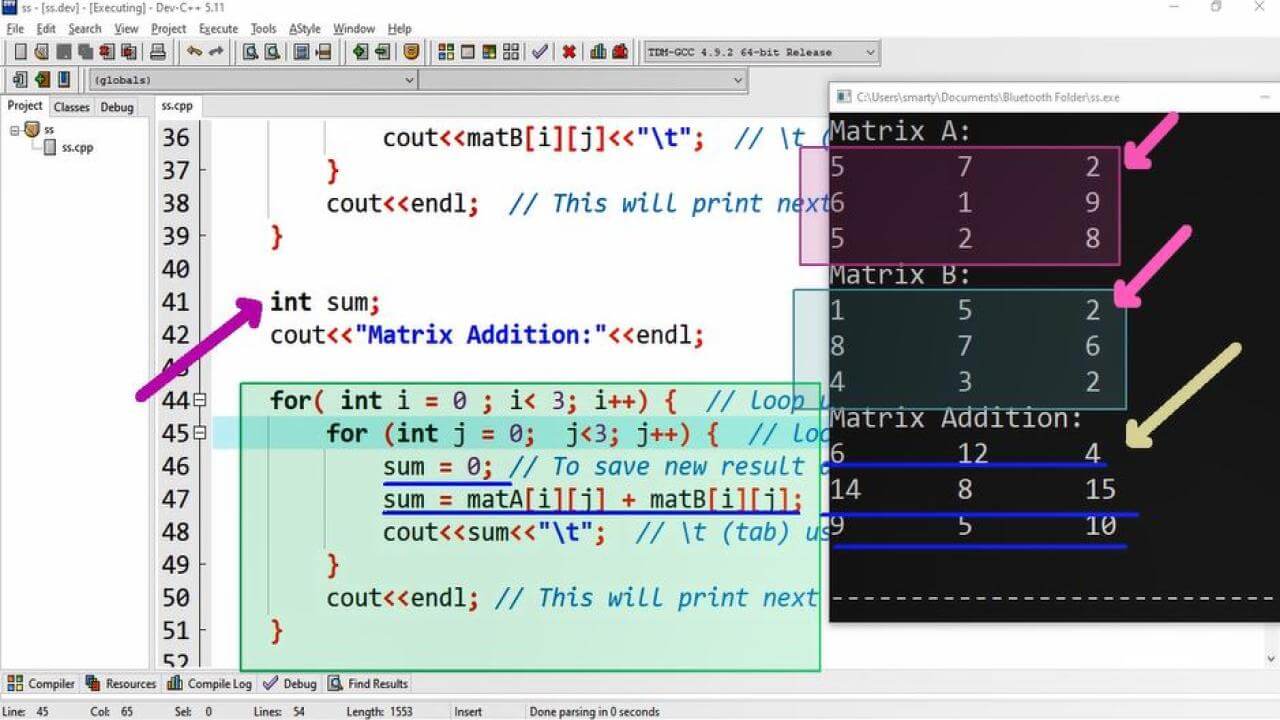
Working:

This program is compiled and tested using Dev-C++. In this source code first of we have declared two matrices of order 3 x 3. As their is constrain in matrix addition that both matrices must be of same order. So that we initialize these matrices of order 3 x 3 by random values.

After initialization of matrices we display their values using nested for loop one by one. Then we use netsed loop to get sum of matrices and print their sum. In this nested loop we declare asum variable of int data type. Each time in inner loop we assign it value 0. So that it will carry new addition of particular elements of matrices.Here we have used \t tab escape sequence for printing proper sapce in between elements of matrix rows.